集合运算

集合运算包括^（交集）、&（并集）、\（差集）、|（合集）等，比如：

	A	B
1	[a,b,1,2,3,4]	[d,b,10,12,3,4]
2	=A1^B1	=A1\B1
3	=A1&B1	=A1|B1

A1与B1中的序列如下：

 

A2,B2,A3,B3中，分别计算这两个序列的交集，差集，并集和合集。计算后，A2,B2,A3,B3中的结果分别如下：

    

说明：并集与合集都是把两个序列的成员按顺序合并起来组成新序列，但并集中共同的成员不重复出现，合集中会重复出现。

在上面的集合运算中，序列中包含了不同种类的数据，既有字符，又有整数。双目运算只需比较是否相等，因此上面的代码能够正常运行，但需要注意的是，字符与整数是不能比较大小的。如果需要比较大小，如计算排序等，必须保证序列内成员数据能够比较。如：

	A	B	C
1	[3.456,5L,,2,-3,4]	=["d","b","Ace",,"Tom","3"]	[a,b,1,2,3,4]
2	=A1.sort@z()	=B1.sort()	=C1.sort()

A1中序列的成员包括各种实数及空值，B1中的成员包括字符串或空值，A1与B1中的成员均可以比较。A2与B2中排序后的结果如下：

 

其中，空值null都会被认为是最小值。

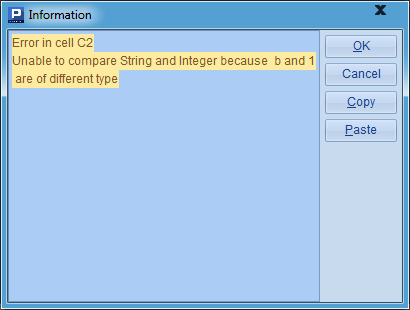
C1中的序列中，既包括字符串，又包括整数，两种类型的数据是不能比较的，因此C2在计算时会报错：

对位四则运算

长度相同的两个序列可按成员进行对位计算，返回序列，包括：++（加）、--（减）、**（乘）、//（除）、（求余）%%，比如：

	A	B
1	[1,2,3,4]	[10,12,3,4]
2	=A1++B1	=A1--B1
3	=A1**B1	=A1//B1

A1与B1中的序列如下：

 

A2,B2,A3,B3中，分别用这两个序列计算对位加法，对位减法，对位乘法和对位除法。计算后，A2,B2,A3,B3中的结果分别如下：

    

布尔运算

在集算器中，用函数cmp(A,B)可以比较两个序列A与B的大小。

Ø  cmp(A,B)

比较序列大小时，对位比较每个成员的值，遇到第一个不等成员时根据大小分别返回1或-1，A与B全等则返回0。特别的，cmp(A)或者cmp(A,0)，表示A和与之等长且成员均为0的数列比较，即cmp(A,[0,0,…,0])。

	A
1	=cmp(["a","b","c"],["a","b","c"])
2	=cmp([1,3,5,7],[1,3,7,5])
3	=cmp([7,6,5,4],[7,6,4,10,11])

A1,A2和A3中结果如下：

   

两个序列的比较可以简写成A==B, A>B这样的形式。

通过使用这种写法，两个序列可以对位比较其大小，结果为布尔型。如：

	A
1	=[1,2,3]==[1,2,3]
2	=[1,"B",3]<=[1,"b",4]
3	=[1,2,3]<[1,3,4]

A1中比较结果为true，两个序列相等。A2中比较结果为true，因为B比b小。A3中结果为true，因为两个序列的第2个成员比较时，2比3要小：

   

需要注意的是，集算器中的序列，是有序的集合，因此在判断两个序列A与B是否大小相等时，是跟顺序有关的。如果需要判断的是两个序列是否有着相同的成员，需要用A.eq(B)来判断：

	A
1	[Tom,Jerry,Tuffe,Tyke]
2	[Jerry,Tuffe,Tom,Tyke]
3	=A1==A2
4	=A1.eq(A2)

A1和A2中成员的顺序不同，因此A3中的结果表明两个序列不相等：

A4中的结果为true，说明两个序列的成员相同：